---

拉格朗日函数的对偶问题

原始问题

针对有等式和不等式约束的最优化原始问题：

$$\underset{x}{min}f(x) \\ s.t.\quad h_i(x)=0,i=1,2,...,m \\ s.t.\quad g_j(x)\leq0,j=1,2,...,n \tag{1-1}$$

文章拉格朗日乘子法与L1和L2正则项中给出了它的拉格朗日方程：

$$L(x,\alpha,\beta)=f(x)+\sum^m_{i=1}\alpha_ih_i(x)+\sum^n_{j=1}\beta_jg_j(x) \tag{1-2}$$

$\alpha_i$和$\beta_j$为拉格朗日乘子，根据不等式约束的拉格朗日乘子条件知道$\beta_j\geq0$。

对于(2)式，假设给定一个不符合原始问题(1)约束条件的$x$(即存在$i$使得$h_i(x)\neq0$，或者存在$j$使得$g_j(x)>0$)，若存在$h_i(x)\neq0$，可令$\alpha_i \rightarrow\infty$，若存在$g_j(x)>0$，可令$\beta_j \rightarrow\infty$，则一定有：

$$\underset{\alpha,\beta;\alpha_i\geq0}{max}[f(x)+\sum^m_{i=1}\alpha_ih_i(x)+\sum^n_{j=1}\beta_jg_j(x) ]\rightarrow\infty \tag{1-3}$$

给定一个符合原始问题(1)约束条件的$x$，即$h_i(x)=0$且$g_j(x)\leq0$，一定会存在：

$$\underset{\alpha,\beta;\alpha_i\geq0}{max}[f(x)+\sum^m_{i=1}\alpha_ih_i(x)+\sum^n_{j=1}\beta_jg_j(x) ]=f(x) \tag{1-4}$$

此时$h_i(x)=0$，对于$g_j(x)$它最大值在它为0的时候取到

由此看到只有当所有$x$必须满足约束条件时，问题才会有解，否则，(3)式可令结果为无穷导致问题无解。

则根据(1-1)公式和(1-4)得到等价问题，它们有相同的解：

$$\underset{x}{min}\underset{\alpha,\beta;\beta_j\geq0}{max}L(x,\alpha,\beta) \tag{1-5}$$

定义原始问题的最优值：

$$\underset{x}{min}\underset{\alpha,\beta;\beta_j\geq0}{max}L(x,\alpha,\beta)=p^{*} \tag{1-6}$$

对偶问题

为了找到对偶的问题，则定义一个对偶函数，令：

$$D(\alpha,\beta)=\underset{x}{min}L(x,\alpha,\beta) \tag{1-7}$$

有了对偶函数就可给出对偶问题了，与原始问题的形式非常类似，只是把min和max交换了一下，加上限制条件：

$$\underset{\alpha,\beta;\beta_j\geq0}{max}D(\alpha,\beta)=\underset{\alpha,\beta;\beta_j\geq0}{max}\underset{x}{min}L(x,\alpha,\beta) \\ s.t. \quad \beta_j\geq0,j=1,2...,m \tag{1-8}$$

$\alpha$和$\beta$称为对偶变量，定义对偶函数的最优值

$$\underset{\alpha,\beta;\beta_j\geq0}{max}D(\alpha,\beta)=d^{*} \tag{1-9}$$

若原始问题与对偶问题都有最优解，则：

$$d^{*}=\underset{\alpha,\beta;\beta_j\geq0}{max}\underset{x}{min}L(x,\alpha,\beta) \leq \underset{x}{min}\underset{\alpha,\beta;\beta_j\geq0}{max}L(x,\alpha,\beta)=p^{*} \tag{1-10}$$

• 当$d^*\leq p^*$，称为“弱对偶性(weak duality)”成立，对于所有优化问题都成立，即使原始问题非凸；
• 当$d^*=p^*$，则称为“强对偶性(strong duality)”成立。

强对偶是一个非常好的性质，因为在强对偶成立的情况下，可以通过求解对偶问题来得到原始问题的解，在SVM中就是这样做的。当然并不是所有的对偶问题都满足强对偶性，在SVM中是直接假定了强对偶性的成立，其实只要满足一些条件，强对偶性是成立的，比如说Slater条件与KKT条件。

Slater条件:对于原始问题及其对偶问题，假设函数$f(x)$和$g_j(x)$是凸函数，$h_i(x)=0$为仿射函数，且不等式约束$g_j(x)$是严格可行的(即存在$x$，对所有$j$有$g_j(x)<0$)，则存在$x^*,\alpha^*,\beta^*$，使$x$是原始问题的解，$\alpha^*,\beta^*$是对偶问题的解，并且:

$$p^{*}=d^{*}=L(x^{*},\alpha^{*},\beta^{*})$$

也就是说如果原始问题是凸优化问题并且满足 Slater 条件的话，那么强对偶性成立。需要注意的是，这里只是指出了强对偶成立的一种情况，并不是唯一的情况。

假如有$\vec{x}\in\mathbb{R}^n,\vec{b}\in\mathbb{R}^m$，矩阵$A_{m\times n}$，那么：

$$\vec{x}\rightarrow A\vec{x}+\vec{b}$$

被成为$\mathbb{R}^n \rightarrow \mathbb{R}^m$的仿射变换，这一过程被称为仿射函数。

$$f(x)=Ax+b,x\in \mathbb{R}^n$$

比如最简单的$a_1x_1+a_2x_2+\cdots +a_nx_n+b$
就是一个仿射函数。仿射函数有一个非常重要的性质，那就是它既凹又凸。

---

支持向量机

基本型

支持向量机(Support Vector Machine,SVM)是在深度学习出现之前应用十分广泛一种机器学习二分类的算法，它通过求解超平面来划分不同类别的样本。
假设给定一些样本点，这些样本点可以通过超平面分割，我们要找到一个最好的超平面。下面假设样本点只有两个维度$x_1$和$x_2$，那么就是找到一条最优的直线划分这两类样本。

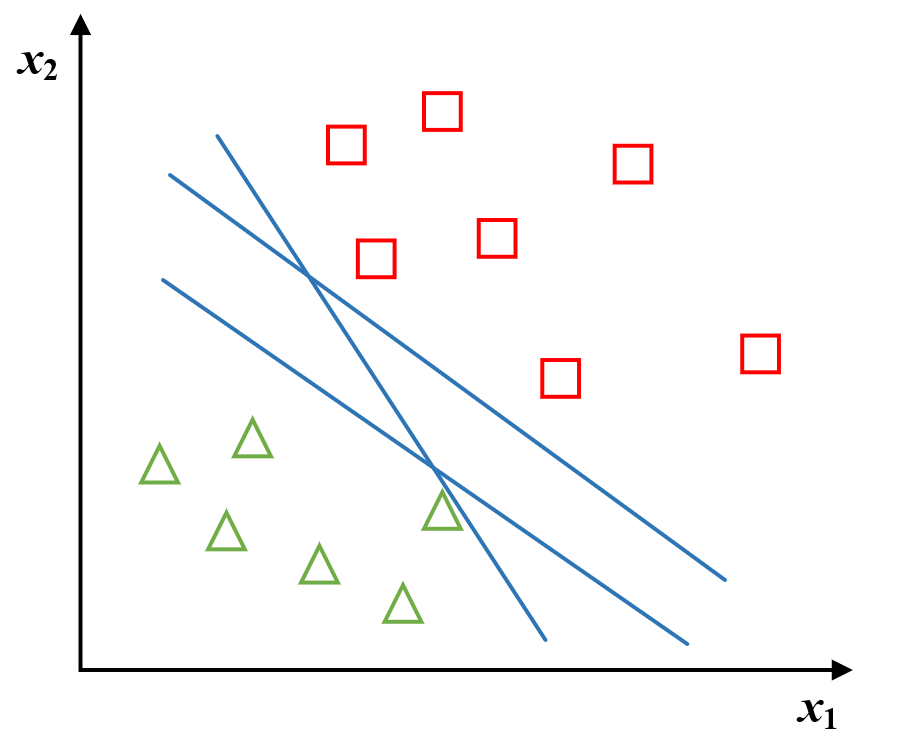
上图中，有三条直线去划分样本点，从直觉来看它们都不是最好的，它们距离样本太近，泛化能力差，所以我们要找到一条直线，使得所有的点距离它都最远。

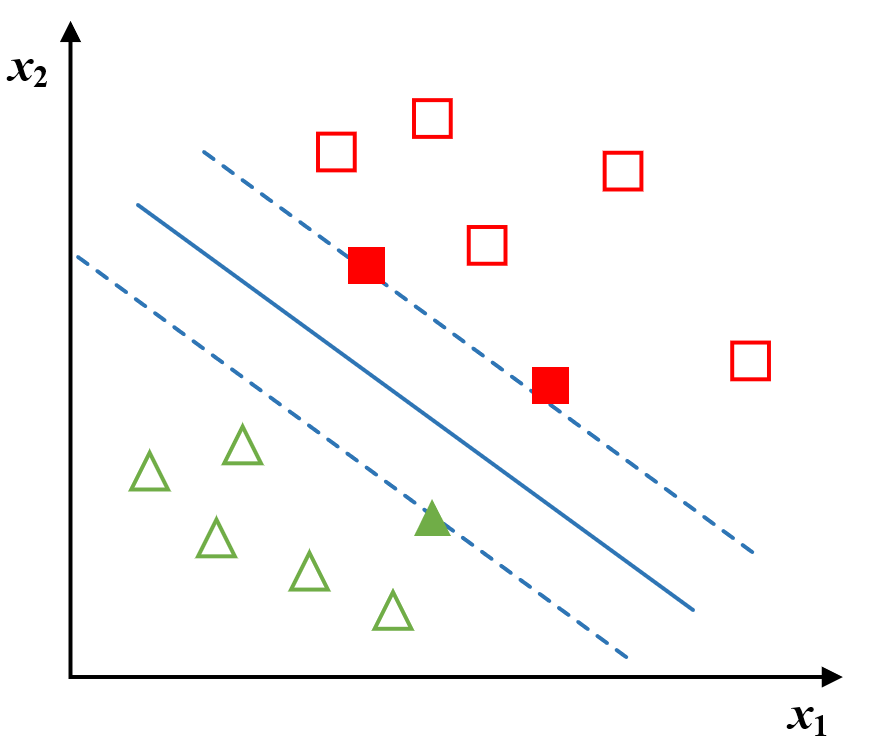
如上图，我们需要找到一条直线(图中的中间蓝色实线)，对于离群样本点有更好的兼容性，鲁棒性更好，即泛化能力更好。推广到更高的维度，就是说我们要找到一个超平面，将样本点更好的区分开来。

设样本空间为$D=\{(x_1,y_1),(x_2,y_2),…,(x_N,y_N)\},y_i \in \{+1,-1\},i=1,2,…,n$，$x_i$为第$i$个样本，$y_i$为$x_i$的分类，当$y_i=+1$时，$x_i$分类为$+1$(正样本)，对应上图右上角的的正方形样本，$x_i$分类为$-1$(负样本)，对应上图的左上角三角形样本。
假设超平面的函数为(上图的蓝色实线)：

$$w^T\cdot x+b=0 \tag{2-1}$$

其中$w=(w_1,w_2,..,w_n)$为法向量，决定了超平面的方向，$b$为位移项，决定了超平面与原点之间的距离。
回忆点到直线的距离，点$(x_0,y_0)$到$Ax+By+C=0$的距离：

$$d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} \tag{2-2}$$

推广到n维空间$\theta^Tx_b=0$，可以得到任意点$x$到超平面$w^Tx+b=0$的距离为：

$$d=\frac{|w_Tx+b|}{\sqrt{w_1^2+w_2^2+...+w_N^2}}=\frac{|w_Tx+b|}{\left \|w\right \|} \tag{2-3}$$

假设超平面$w^Tx+b=0$可以对样本进行正确分类，那么对于$(x_i,y_i)\in D$，有：

$$\left\{\begin{matrix} w^Tx+b>0 \quad if \quad y_i=+1 \\ w^Tx+b<0 \quad if \quad y_i=-1 \end{matrix}\right. \tag{2-4}$$

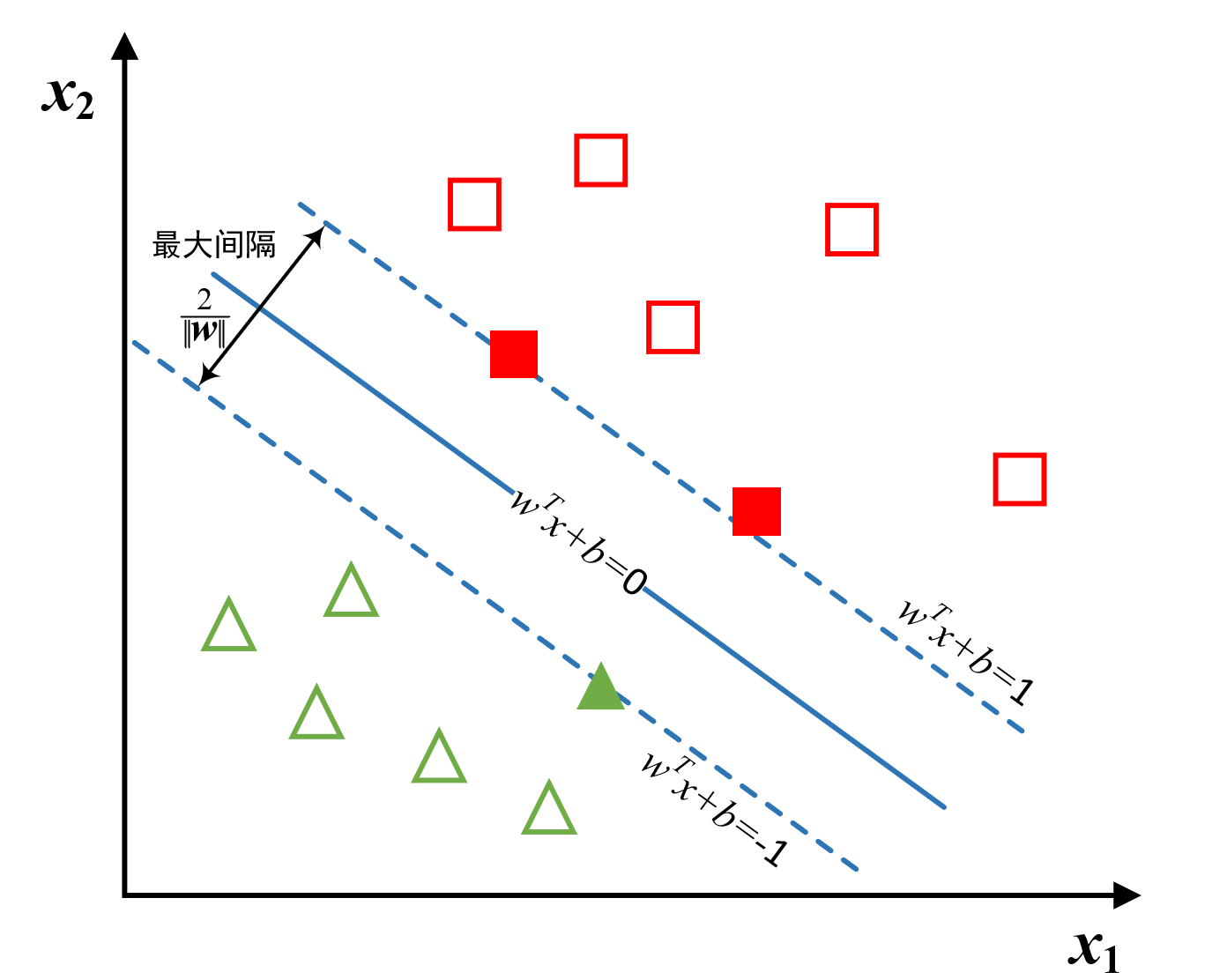
我们给svm留点空间，假设：

$$\left\{\begin{matrix} w^Tx+b>+1 \quad if \quad y_i=+1 \\ w^Tx+b<-1 \quad if \quad y_i=-1 \end{matrix}\right. \tag{2-5}$$

上图中，那些实心的样本位于这两个超平面之上(图上的蓝色虚线)，我们称为“支撑向量”，两个超平面之间的距离叫做间隔，根据平面之间的距离公式有：

$$d=\frac{2}{\left \|w\right \|} \tag{2-6}$$

为了能够找到一个最好的超平面划分两类样本，我们应该最大化这个间距$d$，即：

$$\underset{w,b}{max}\frac{2}{\left \|w\right \|} \tag{2-7}$$

最大化$d$就相当于最小化$\left |w\right |$，为了方便导数运算，我们得到和最大化$d$等价的运算：

$$\underset{w,b}{min}\frac{1}{2}\left \|w\right \|^2 \tag{2-8}$$

接下来把公式(2-5)进行变形，得到$y_i(w^Tx+b)\geq1,i=1,2,…,n$，最后我们得到svm的基本型：

$$\begin{aligned} &\underset{w,b}{min}\frac{1}{2}\left \|w\right \|^2 \\ &s.t. \quad y_i(w^Tx+b)\geq1,i=1,2,...,n \end{aligned} \tag{2-9}$$

这不就是一个不等式约束的问题吗，接下来我们构造拉格朗日公式：

$$L(w,b,\beta)=\frac{1}{2}\left \|w\right \|^2+\sum^N_{i=1}\beta_i(1-y_i(w^Tx_i+b)) \tag{2-10}$$

其中，$\beta=(\beta_1,\beta_2,…,\beta_n)$，不等式约束拉格朗日乘子约束$\beta_i\geq0$

对偶型

根据上文提到的拉格朗日对偶的问题，我们转化为(1-5)式有：

$$\underset{w,b}{min}\underset{\beta_i\geq0}{max}L(w,b,\beta) \tag{2-11}$$

交换下最小和最大的位置，转化为对偶问题，得到：

$$\underset{\beta_i\geq0}{max}\underset{w,b}{min}L(w,b,\beta) \tag{2-12}$$

而svm满足KKT条件，它具备强对偶性，所以解决掉(2-12)的最优解就可以求得基本型(2-9)的最优解，对(2-10)的$w,b$分别求偏导并令导数为0，得到：

$$\begin{aligned} \frac{\partial L(w,b,\beta)}{\partial w}=w-\sum^N_{i=1}\beta_iy_ix_i=0 \\ \frac{\partial L(w,b,\beta)}{\partial b}=\sum^N_{i=1}\beta_iy_i=0 \end{aligned} \tag{2-13}$$

将(2-13)代入拉格朗日公式(2-10)，消去$w,b$，得到(2-10)的对偶问题：

$$\begin{aligned} &\underset{\beta_i\geq0}{max}\sum^N_{i=1}\beta_i-\frac{1}{2}\sum^N_{i=1}\sum^N_{j=1}\beta_i\beta_jy_iy_jx_i^ Tx_j \\ &s.t. \quad \sum^N_{i=1}\beta_iy_i=0 \\ &s.t. \quad \beta_i\geq0,i=1,2,...,N \end{aligned} \tag{2-14}$$

推导至这一步，已经可以通过样本计算出$\beta_i$的值，然后根据$\beta_i,w,b$的关系求出模型：

$$\begin{aligned} f(x)&=w^Tx+b \\ &=(\sum^N_{i=1}\beta_iy_ix_i)^Tx+b \end{aligned} \tag{2-15}$$

对于b，选择部位0的$\beta_i$代入公式(2-15)，得到：

$$b=y_i-\sum^N_{i=1}\beta_iy_ix_i^Tx_j \tag{2-16}$$

最后，支持向量机的决策边界函数，仅由$\beta_i \neq 0$的向量所决定，即仅有在边界函数上的点所决定，决策边界为：

$$w^Tx+b=0 \tag{2-17}$$