---

Gradients

该部分介绍了雅可比矩阵、链式求导法则，最后推算出下图的输出得分$s$对$W$和$b$的求导结果。

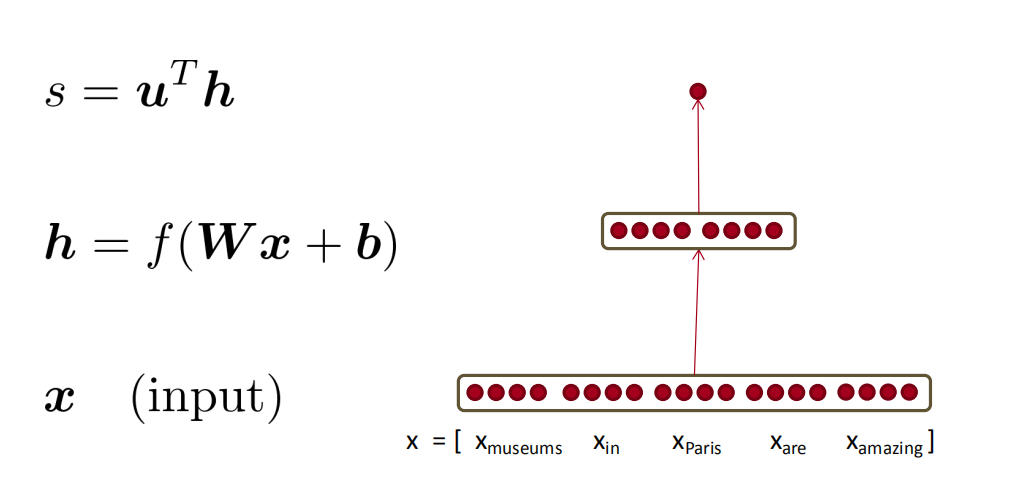
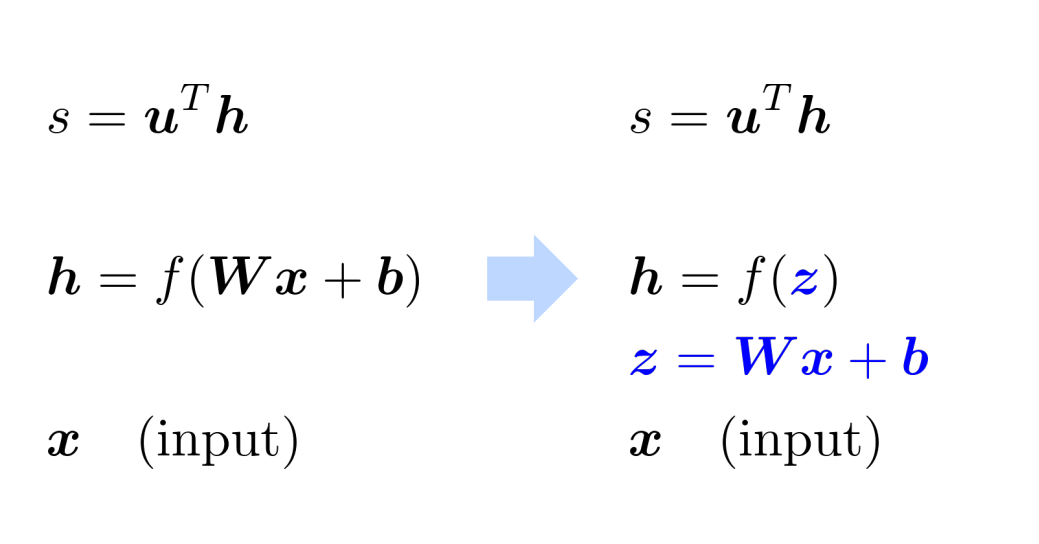
根据链式求导法则 :

$$\frac{\partial s}{\partial b}=\frac{\partial s}{\partial h}\frac{\partial h}{\partial z}\frac{\partial z}{\partial b}=u^Tdiag(f'(z))I=u^T \cdot f'(z)$$ $$\frac{\partial s}{\partial W}=\frac{\partial s}{\partial h}\frac{\partial h}{\partial z}\frac{\partial z}{\partial W}$$

令$\delta=\frac{\partial s}{\partial h}\frac{\partial h}{\partial z}=u^T \cdot f’(z)$，$\delta$是局部误差符号，则

$$\frac{\partial s}{\partial W}=\delta\frac{\partial z}{\partial W}=\delta^T x^T$$ $$\frac{\partial s}{\partial b}=\delta\frac{\partial z}{\partial b}=\delta$$

Derivative with respect to Matrix: Output shape

$W \in \mathbb{R}^{n \times m},\frac{\partial s}{\partial W}$的形状是啥?
我们遵循导数的形状是参数的形状的规则，可以看到它是一个$n \times m$的雅可比矩阵

$$\begin{bmatrix} \frac{\partial s}{\partial W_{11}} & \cdots & \frac{\partial s}{\partial W_{1m}}\\ \vdots & \ddots & \vdots \\ \frac{\partial s}{\partial W_{n1}} & \cdots & \frac{\partial s}{\partial W_{nm}} \end{bmatrix}$$

Why the Transposes?

为什么$\frac{\partial s}{\partial W}=\delta^T x^T$中$\delta$是转置?

$$\frac{\partial s}{\partial W}=\delta^T x^T=\begin{bmatrix} \delta_1 \\ \vdots \\ \delta_n \end{bmatrix} [x_1,...,x_m]=\begin{bmatrix} \delta_1x_1 & \cdots & \delta_1x_m\\ \vdots & \ddots & \vdots \\ \delta_nx_1 & \cdots & \delta_nx_m \end{bmatrix}$$

---

Deriving local input gradient in backprop

通过神经网络展开的图计算$\frac{\partial s} {\partial W}$

$$\frac{\partial s}{\partial W}=\delta\frac{\partial z}{\partial W}=\delta \frac{\partial}{\partial W}Wx+b$$

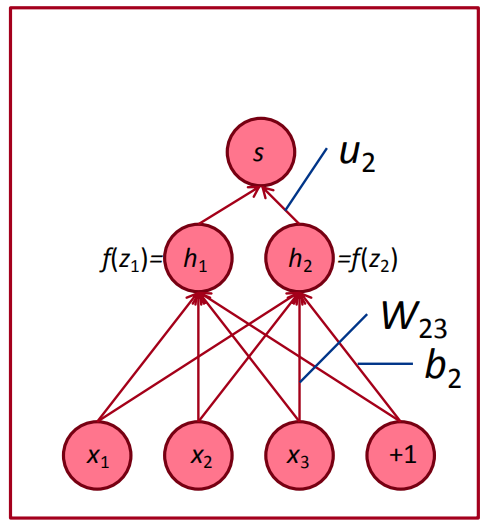
我们只考虑$W_{ij}$的导数，$W_{ij}$只对$z_i$有贡献，例如$W_{23}$只对$z_2$有贡献，对$z_1$没有贡献，可推导出 ：

$$\frac{\partial z_i}{\partial W_{ij}}=\delta \frac{\partial}{\partial W_{ij}}W_ix+b_i=\frac{\partial}{\partial W_{ij}}\sum^d_{k=1}W_{ik}x_k=x_j$$

---

Backpropagation

前向传播(从左至右计算)

$$s=u^Th$$ $$h=f(z)$$ $$z=Wx+b$$ $$x(input)$$

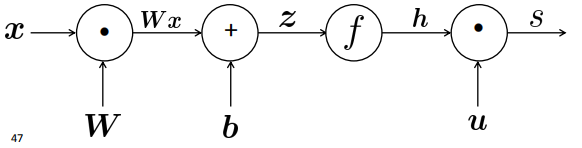
后向传播(从右至左传递导数)

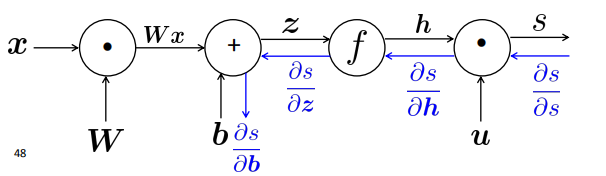
Backpropagation: Single Node

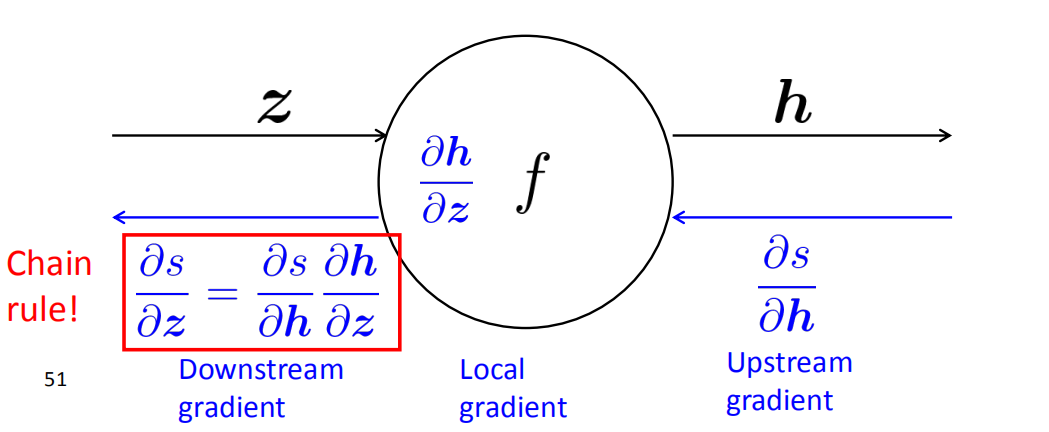
• 节点接收“上游梯度”
• 目标是传递正确的“下游梯度”
• 每个节点都有局部梯度local gradient，它输出的梯度是与它的输入有关
• [downstream gradient] = [upstream gradient] x [local gradient]

• 多个输入对应多个局部梯度

  An Example

$$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial a}\frac{\partial a}{\partial x}=2$$ $$\frac{\partial f}{\partial y}=\frac{\partial f}{\partial a}\frac{\partial a}{\partial y}+\frac{\partial f}{\partial b}\frac{\partial b}{\partial y}=2+3=5$$ $$\frac{\partial f}{\partial z}=0$$

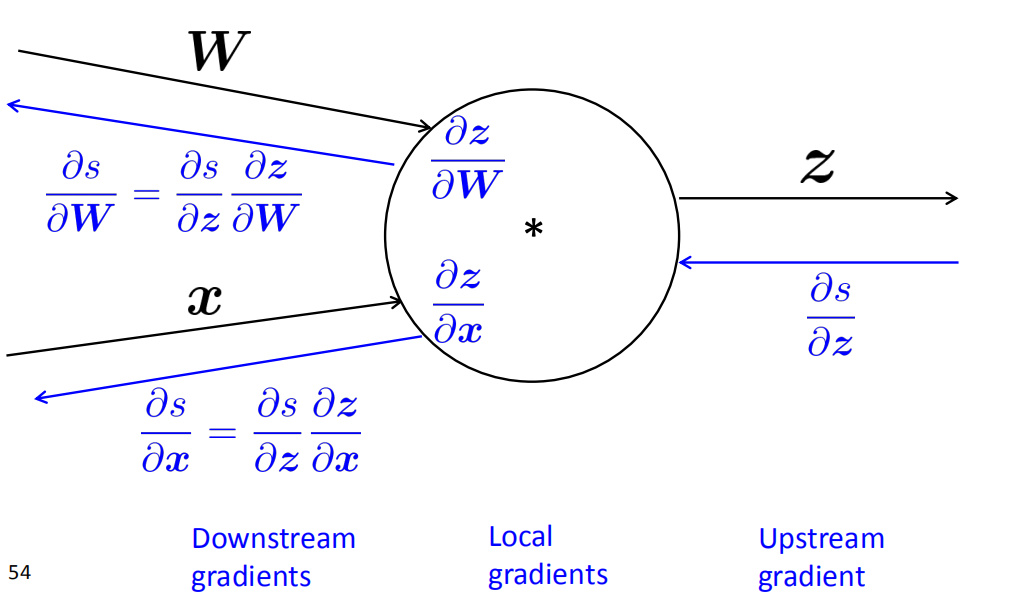
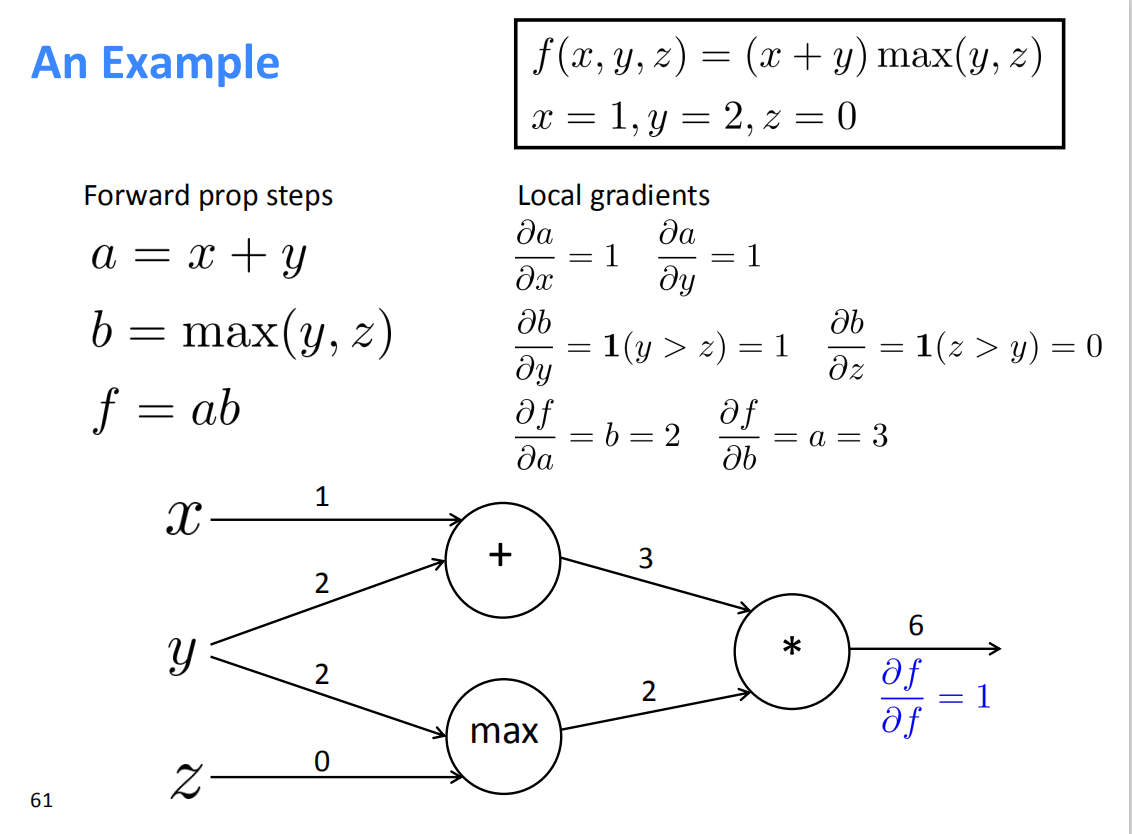
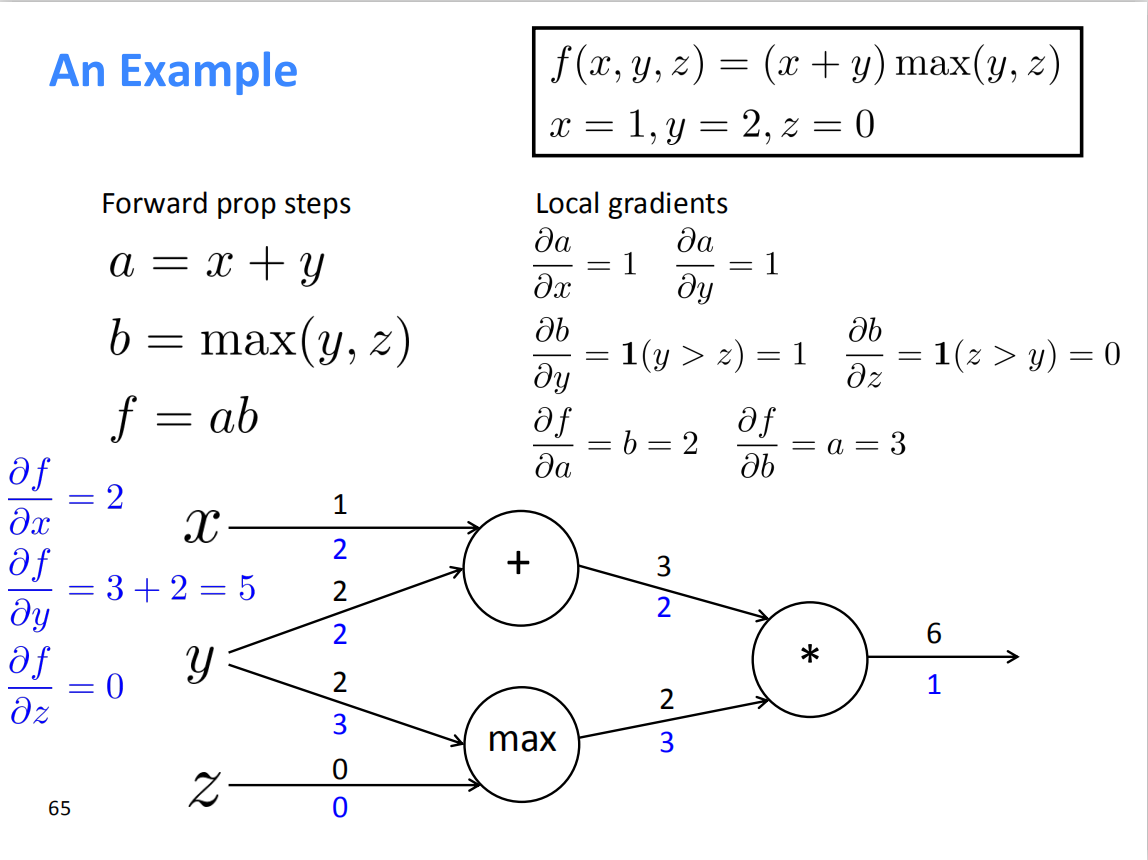
Efficiency: compute all gradients at once

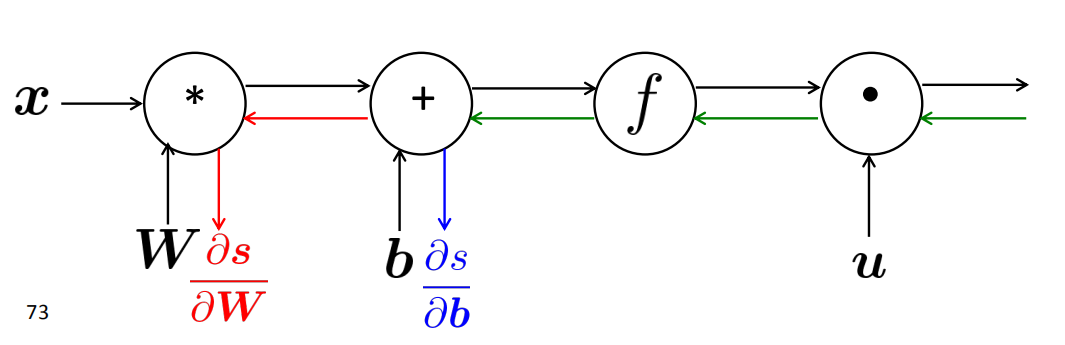
• 绿的线的部分导数可以共用以此减少计算

Back-Prop in General Computation Graph

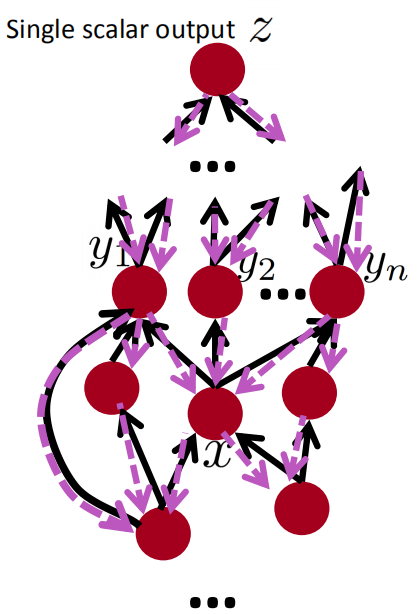
1. Fprop：按拓扑排序顺序访问节点
   • 计算给定父节点的节点的值
2. Bprop：
   • 初始化输出梯度为 1
   • 以相反的顺序方位节点，使用节点的后继的梯度来计算每个节点的梯度
   • $\{y_1,y_2,…,y_n\}$是$x$的后继
   • $\frac{\partial z}{\partial x}=\sum^n_1\frac{\partial z}{\partial y_i}\frac{\partial y_i}{\partial x}$
   • 正确地说，Fprop 和 Bprop 的计算复杂度是一样的
   • 一般来说，我们的网络有固定的层结构，所以我们可以使用矩阵和雅可比矩阵

Automatic Differentiation

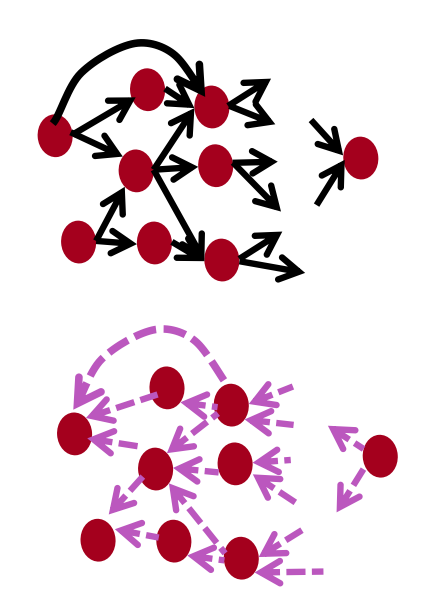
• 梯度计算可以从 Fprop 的符号表达式中自动推断
• 每个节点类型需要知道如何计算其输出，以及如何在给定其输出的梯度后计算其输入的梯度
• 现代DL框架(Tensorflow, Pytoch)为您做反向传播，但主要是令作者手工计算层/节点的局部导数

---

Notes 03 Neural Networks, Backpropagation

Neural Networks: Foundations

该部分涉及到DL中的W和b的更新，已经掌握

Neural Networks: Tips and Tricks

此部分已经在我的文章常用图像分类模型和相关的知识点中学习