---

Classification setup and notation

通常我们有由样本组成的训练数据集

$$\{x_i,y_i\}_{i=1}^N$$

$x_i$是输入，例如单词(索引或是向量)，句子，文档等，维度为$d$
$y_i$是我们尝试预测的标签($C$各类别中的一个)，例如 :

• 类别：感情，命名实体，购买/售出的决定
• 其他单词
• 之后：多词序列的

  Classification intuition

训练数据 : $\{x_i,y_i\}_{i=1}^N$
简单的说明情况

• 固定的二维单词向量分类
• 使用softmax/logistic回归
• 线性决策边界

传统的机器学习/统计学方法： 假设$x_i$是固定的，训练softmax/logistic回归的权重$W\in \mathbb{R}^{C\times d}$来决定决策边界(超平面)
方法 : 对每个$x$，预测

$$p(y|x)=\frac{exp(W_y\cdot x)}{\sum_{c=1}^Cexp(W_c\cdot x)}$$

我们可以将预测函数分为两个步骤：

1. 将$W$的第$y$行和$x$中的对应行相乘得到分数，计算所有的$fc,for c=1,…,C$ $$W_y\cdot x=\sum^d_{i=1}W_{yi}x_i=f_y$$
2. 使用softmax函数获得归一化的概率 $$p(y|x)=\frac{exp(f_y)}{\sum^C_{c=1}exp(f_c)}$$

   Training with softmax and cross-entropy loss

   对于每个训练样本$(x,y)$，我们的目标是最大化正确类$y$的概率，或者我们可以最小化该类的负对数概率 $$-logp(y|x)=-log(\frac{exp(f_y)}{})$$

   Background: What is “cross entropy” loss/error?

• 交叉熵的概念来源于信息论，衡量两个分布之间的差异
• 令真实概率分布为$p$
• 令我们计算的模型概率为$q$
• 交叉熵为 $$H(p,q)=-\sum^C_{c=1}p(c)logq(c)$$
• 假设groud truth(or true or gold or target)的概率分布在正确的类上为1，在其他任何地方为0 ：$p=[0,…,0,1,0,…0]$
• 因为p是one-hot向量，所以唯一剩下的项是真实类的负对数概率

Classification over a full dataset

在整个数据集$\{x_i,y_i\}_{i=1}^N$上的交叉熵损失函数，是所有样本的交叉熵的均值

$$J(\theta)=\frac{1}{N}\sum^N_{i=1}-log(\frac{e^{f_{yi}}}{\sum^C_{c=1}e^{f_c}})$$

我们不使用

$$f_y=f_y(x)=W_y\cdot x=\sum^d_{j=1}W_{yj}x_j$$

我们使用矩阵来表示$f$

$$f=Wx$$

Traditional ML optimization

• 一般机器学习的参数$\theta$通常只由W的列组成 $$\theta=[W_1,...,W_d]=W(:)^T\in \mathbb{R}^{Cd}$$
• 因此，我们只通过以下方式更新决策边界 $$\bigtriangledown_{\theta}J(\theta)=[\bigtriangledown_{W_1},...,\bigtriangledown_{W_d}]^T\in \mathbb{R}^{Cd}$$

---

Neural Network Classifiers

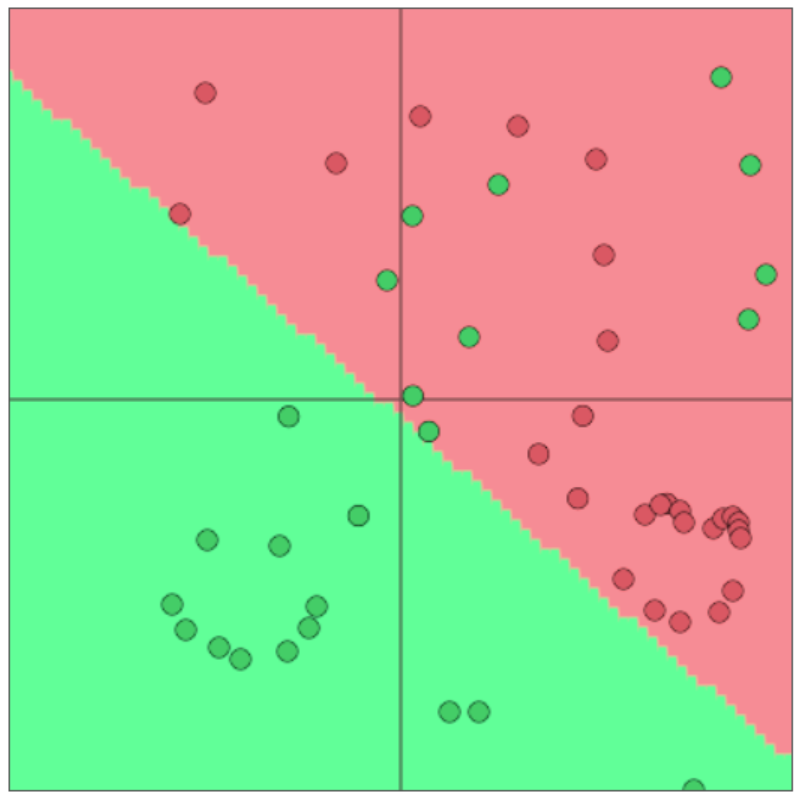
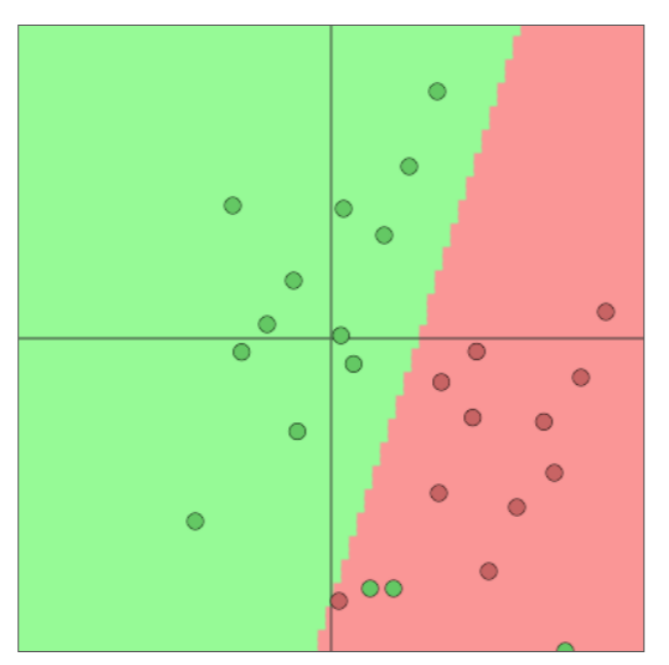
• 单独使用Softmax(≈logistic回归)并不十分强大
• Softmax只给出线性决策边界
  • 这可能是相当有限的，当问题很复杂时是无用的
  • 纠正这些错误不是很酷吗?

Neural Nets for the Win!

神经网络可以学习更复杂的函数和非线性决策边界

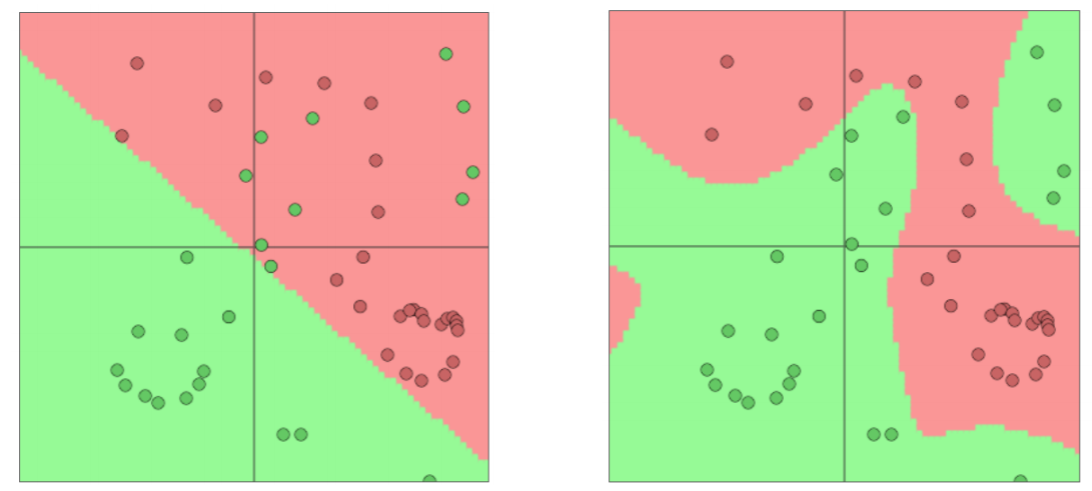
更高级的分类需要

• 词向量
• 更深层次的深层神经网络

  Classification difference with word vectors

  一般在NLP深度学习中
• 我们学习了矩阵$W$和词向量$x$
• 我们学习传统参数和表示
• 词向量是对one-hot向量的重新表示，在中间层向量空间中移动它们，以便使用(线性)softmax分类器通过x = Le层进行分类
  • 即将词向量理解为一层神经网络，输入单词的one-hot向量并获得单词的词向量表示，并且我们需要对其进行更新。其中，$Vd$是数量很大的参数 $$\bigtriangledown_{\theta}J(\theta)=[\bigtriangledown_{W_1},...,\bigtriangledown_{dardvark},...\bigtriangledown_{W_d}]^T\in \mathbb{R}^{Cd+Vd}$$

    Neural computation

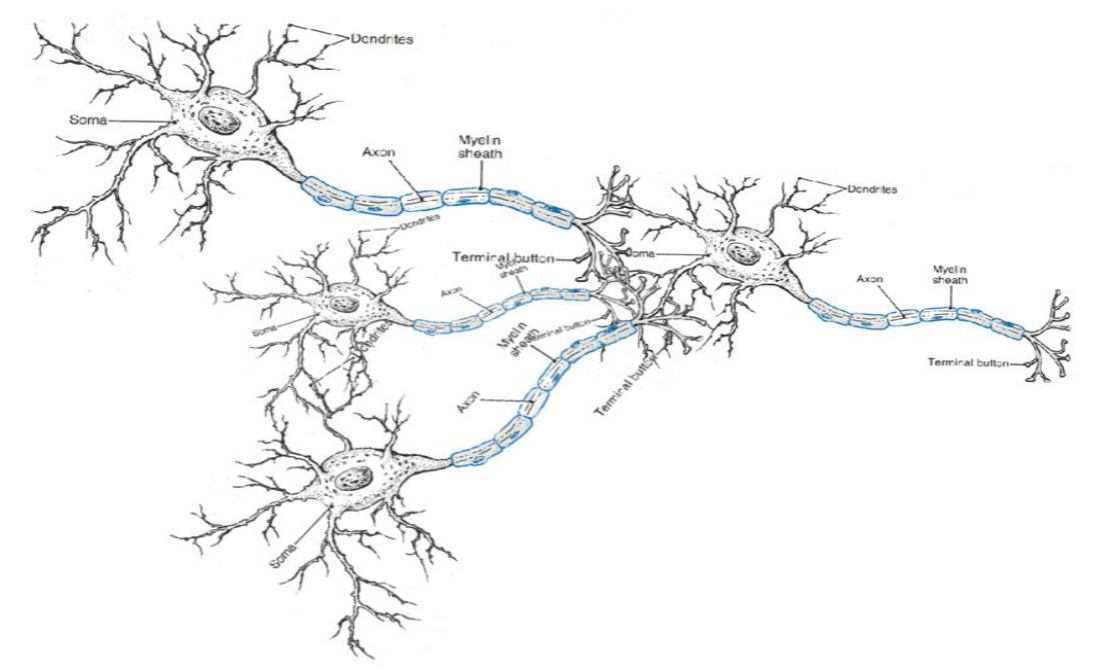
A neuron can be a binary logistic regression unit

$f$为非线性激活函数(例如sigmoid函数)，$w$为权重向量，$b$为偏置向量，$h$为隐藏层变量对应的向量，$x$为输入向量

$$h_{w,b}=f(w^Tx+b)$$ $$f(z)=\frac{1}{1+e^{-z}}$$

$b$ : 我们可以有一个“总是打开”的特性，它给出一个先验类，或者将它作为一个偏向项分离出来
$w,b$是神经元的参数

A neural network = running several logistic regressions at the same time

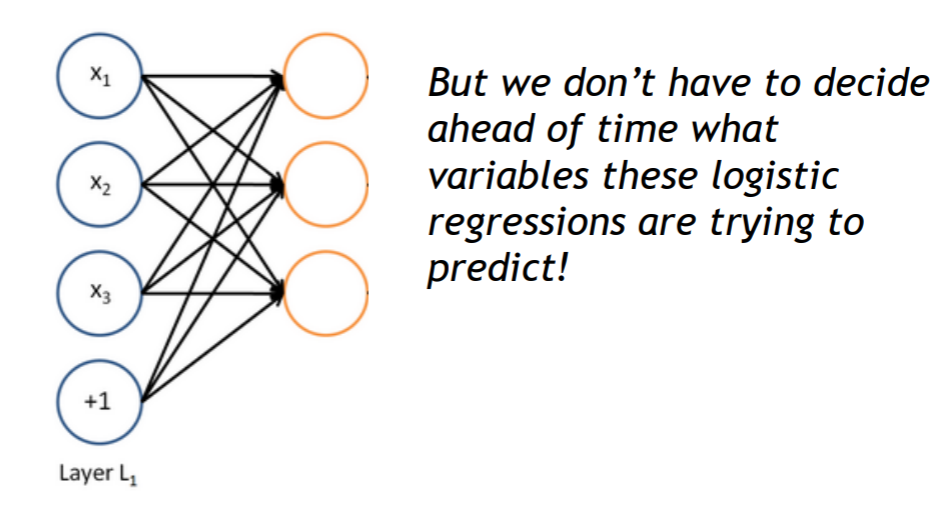
如果我们输入一个向量通过一系列逻辑回归函数，那么我们得到一个输出向量，但是我们不需要提前决定这些逻辑回归试图预测的变量是什么。

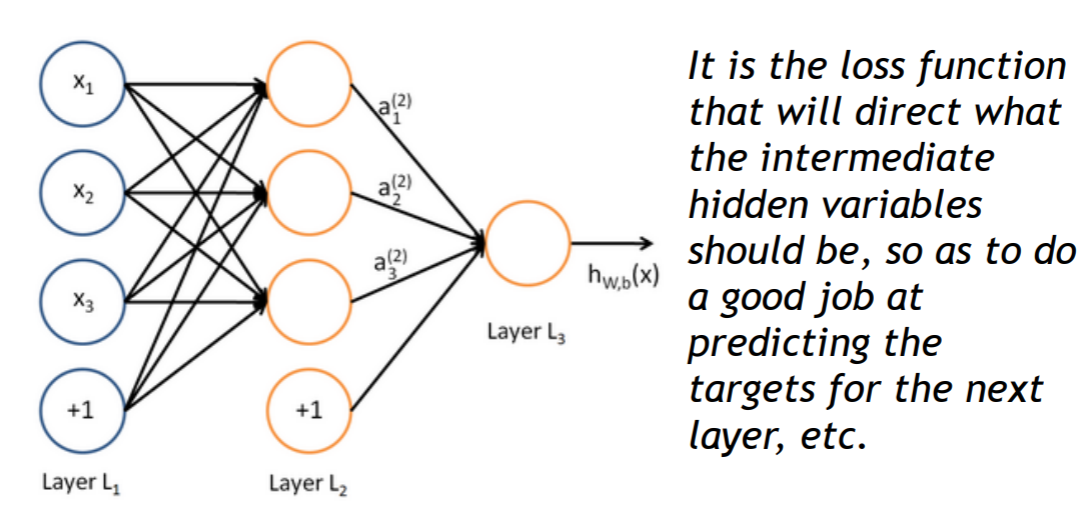
我们可以输入另一个logistic回归函数。损失函数将指导中间隐藏变量应该是什么，以便更好地预测下一层的目标。我们当然可以使用更多层的神经网络。

Matrix notation for a layer

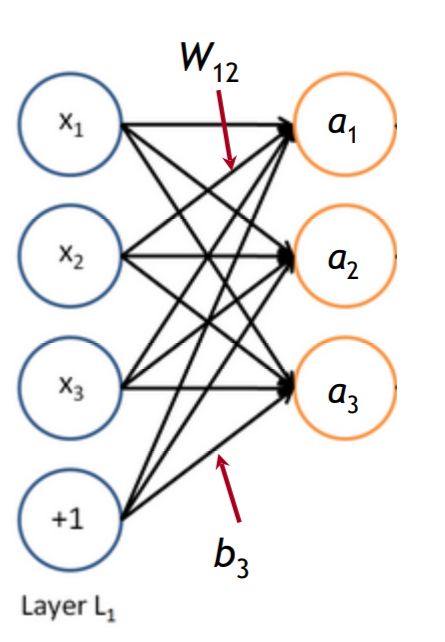
我们有

$$a_1=f(W_11x_1+W_12x_2+W_13x_3+b_1)$$ $$a_2=f(W_21x_1+W_22x_2+W_23x_3+b_2)$$

通过矩阵表示的运算有

$$z=Wx+b$$ $$a=f(z)$$

激活函数$f$在运算时是element-wise逐元素的

$$f([z_1,z_2,z_3])=[f(z_1),f(z_2),f(z_3)]$$

Non-linearities (aka “f ”): Why they’re needed

例如：函数近似，如回归或分类

• 没有非线性，深度神经网络只能做线性变换
• 多个线性变换可以组成一个的线性变换$W_1W_2x=Wx$，因为线性变换是以某种方式旋转和拉伸空间，多次的旋转和拉伸可以融合为一次线性变换
• 对于非线性函数而言，使用更多的层，他们可以近似更复杂的函数

---

Named Entity Recognition (NER)

• 任务：例如，查找和分类文本中的名称

• 可能的用途 :
  • 跟踪文档中提到的特定实体（组织、个人、地点、歌曲名、电影名等）
  • 对于问题回答，答案通常是命名实体
  • 许多需要的信息实际上是命名实体之间的关联
  • 同样的技术可以扩展到其他 slot-filling 槽填充分类
• 通常后面是命名实体链接/规范化到知识库

Named Entity Recognition on word sequences

我们通过在上下文中对单词进行分类，然后将实体提取为单词子序列来预测实体

Why might NER be hard?

• 很难计算出实体的边界

  
  第一个实体是 “First National Bank” 还是 “National Bank”

• 很难知道某物是否是一个实体，是一所名为“Future School” 的学校，还是这是一所未来的学校？

• 很难知道未知/新奇实体的类别

  
  “Zig Ziglar” ? 一个人

• 实体类是模糊的，依赖于上下文

  
  这里的“Charles Schwab” 是 PER 不是 ORG

---

Word window classification

• 思想：在相邻词的上下文窗口中对一个词进行分类
• 例如，上下文中一个单词的命名实体分类(人、地点、组织、NONE)
• 在上下文中对单词进行分类的一个简单方法可能是对窗口中的单词向量进行平均，并对平均向量进行分类(问题是这会丢失单词位置信息)

Window classification: Softmax

• 训练softmax分类器对中心词进行分类，方法是在一个窗口内将中心词周围的词向量串联起来
• 例子：在这句话的上下文中对“Paris”进行分类，窗口长度为2

• 结果$x_{window}=x\in \mathbb{R}^{5d}$是一个列向量

Simplest window classifier: Softmax

对于$x=x_{window}$，我们可以使用与之前相同的softmax分类器

• 如何更新向量？
• 简而言之：求导和优化

Slightly more complex: Multilayer Perceptron

• 在我们的softmax分类器中引入一个附加的非线性层。
• Multilayer Perceptron(mlp)是更复杂的神经系统的基本构件!
• 假设我们要对中心词是否为一个地点，进行分类
• 与word2vec类似，我们将遍历语料库中的所有位置。但这一次，它将受到监督，只有一些位置能够得到高分，在他们的中心有一个实际的NER Location的位置是“真实的”位置会获得高分

  Neural Network Feed-forward Computation

  使用神经激活$a$简单地给出一个非标准化的分数 $$score(x)=U^Ta \in R$$ 我们用一个三层神经网络计算一个窗口的得分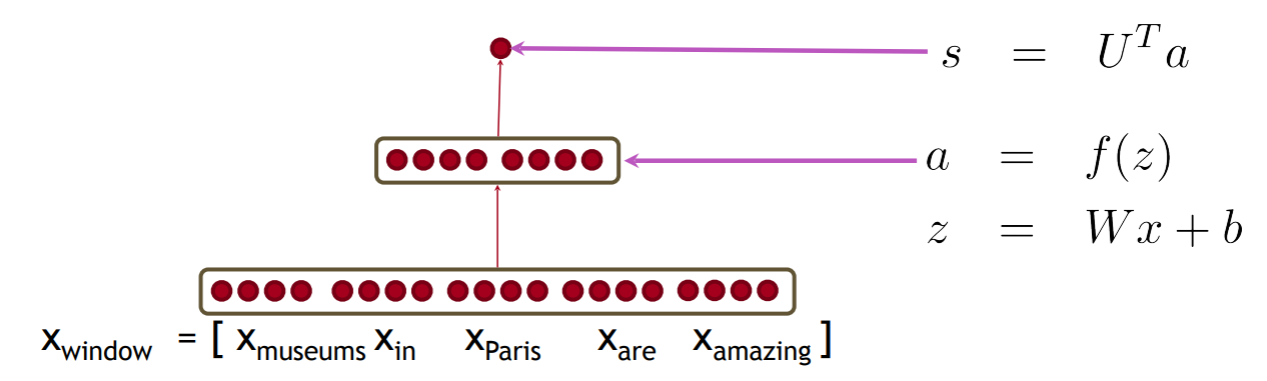 $$s=score("museums in Paris are amazing”)$$ $$s=U^Tf(Wx+b)$$ $$x\in \mathbb{R}^{20 \times 1},W\in \mathbb{R}^{8 \times 20},U\in \mathbb{R}^{8 \times 1}$$

Main intuition for extra layer

中间层学习输入词向量之间的非线性交互
例如：只有当“museum”是第一个向量时，“in”放在第二个位置才重要