01-NLP介绍和词向量

Human language and word meaning

How do we represent the meaning of a word?

用一个词、词组等表示的概念
一个人想用语言、符号等来表达的想法
表达在作品、艺术等方面的思想

理解意义的最普遍的语言方式(linguistic way) : 语言符号与语言符号的意义的转化

How do we have usable meaning in a computer?

WordNet

它是一个包含同义词集和上位词(“is a”关系)synonym sets and hypernyms的列表的辞典

缺点 : 这种表达方式忽略了词在上下文中的语境，缺少新的含义，判断比较主观且无法计算单词间的相似度。

离散向量

最常见的入one-hot编码，传统的自然语言处理中，我们把词语看作离散的符号。单词可以通过独热向量(one-hot vectors，只有一个1，其余均为0的稀疏向量) 。向量维度=词汇量(如500,000)。

$motel = [0,0,0,0,0,0,0,0,0,0,1,0,0,0,0]$ $hotel = [0,0,0,0,0,0,0,1,0,0,0,0,0,0,0]$

缺点 : 所有向量是正交的。对于独热向量，没有关于相似性概念，并且向量维度过大。

词嵌入

一个单词的意思是由经常出现在它附近的单词给出的。
当一个单词$w$出现在文本中时，它的上下文是出现在其附近的一组单词(在一个固定大小的窗口中)。
使用$w$的上下文来构建$w$的表示

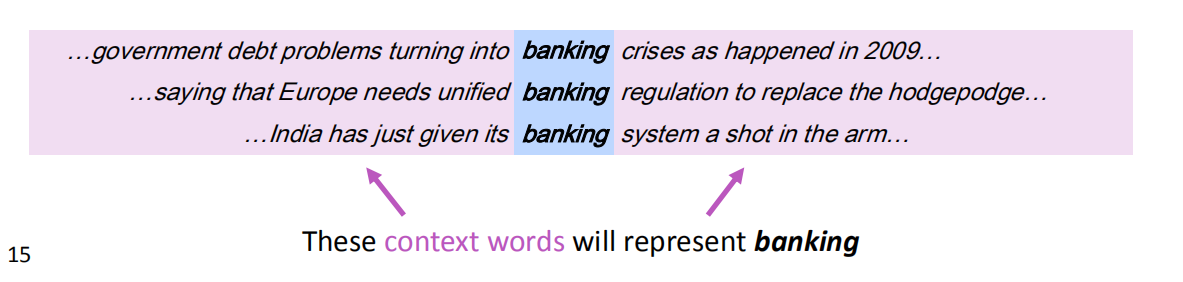
Word2vec introduction

为每个单词构建一个密集的向量，使其与出现在相似上下文中的单词向量相似，词向量word vectors有时被称为词嵌入word embeddings或词表示word representations

Word2vec是一个学习单词向量的框架，它的思路如下 :

有大量的文本
固定词汇表中的每个单词都由一个向量表示
文本中的每个位置$t$，其中有一个中心词$c$和上下文(“外部”)单词$o$
使用$c$和$o$的词向量的相似性来计算给定$c$的$o$的概率(反之亦然)
不断调整词向量来最大化这个概率

下图是窗口大小为$j=2$时的$P(w_{t+j}|w_t)$计算过程，其中center word分别为into和banking

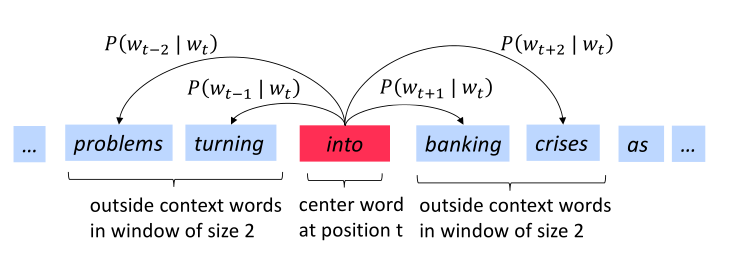
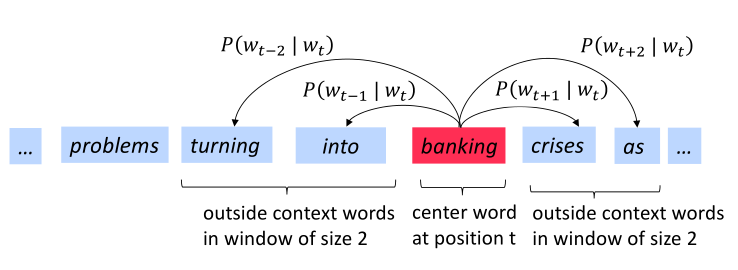
Word2vec objective function

对于每个位置$t=1,…,T$，在大小为m的固定窗口内预测上下文单词，给定中心词$w_j$

$L(\theta)=\prod_{t=1}^{T}\prod_{-m\leq j\leq m,j\neq 0}P(w_{t+j}|w_{t};\theta)$

其中，$\theta$为所有需要优化的变量

损失函数$J(\theta)$是平均负对数似然

$J(\theta)=-\frac{1}{T}logL(\theta)=-\frac{1}{T}\prod_{t=1}^{T}\prod_{-m\leq j\leq m,j\neq 0}logP(w_{t+j}|w_{t};\theta)$

其中log形式是方便将连乘转化为求和，负号是希望将极大化似然率转化为极小化损失函数的等价问题。

连乘转求和 :
$log\prod_{i}x_{i}=\sum_{i}logx_{i}$

上述的$J(\theta)$可以看到我们要让损失函数最小则是让预测更准，即$P(w_{t+j}|w_{t};\theta)$越大

怎么计算$P(w_{t+j}|w_{t};\theta)$？
对于每个单词都是用两个向量，设当单词$w$为中心词的时候的向量为$v_w$，当单词$w$为上下文的某个词的时候向量为$u_w$，$V$为vocab，于是对于一个中心词$c$和一个上下文词$o$有 :

$P(o|c)=\frac{exp(u_o^Tv_c)}{\sum_{w\in V}exp(u_w^Tv_c)}$

公式中，向量$u_o$和向量$v_c$进行点乘。向量之间越相似，点乘结果越大，从而归一化后得到的概率值也越大。模型的训练正是为了使得具有相似上下文的单词，具有相似的向量。

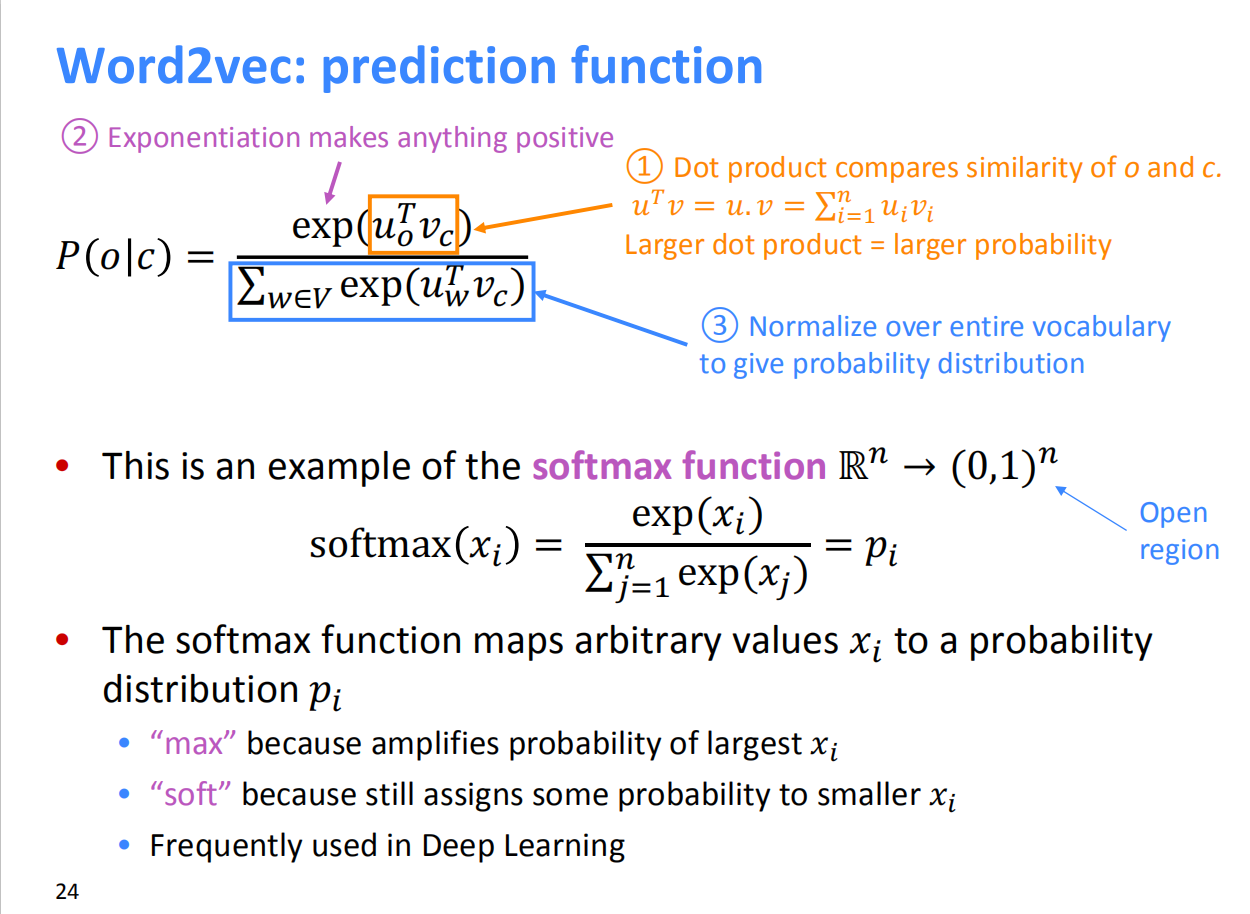
Word2vec prediction function

$P(o|c)=\frac{exp(u_o^Tv_c)}{\sum_{w\in V}exp(u_w^Tv_c)}$

上述公式公式中 :

取幂使任何数都为正
点积比较$o$和$c$的相似性，点积越大则概率越大
分母对整个词汇表进行标准化，从而给出概率分布

将公式做实数集的同等映射$\mathbb{R}^n\rightarrow (0,1)^n$
softmax function :

$softmax(x_i)=\frac{exp(x_i)}{\sum_{j=1}^nexp(x_j)}=p_i$

将任意值$x_i$映射到概率分布$p_i$

max : 因为放大了最大的概率
soft : 因为仍然为较小的$x_i$赋予了一定概率
在深度学习中常用

随机初始化$u_x\in \mathbb{R}^d$和$v_w\in \mathbb{R}^d$，使用梯度下降法进行公式推导

$\begin{aligned} \frac{\partial}{\partial v_clog(o|c)}&=\frac{\partial}{\partial v_c}log\frac{exp(u_o^Tv_c)}{\sum_{w\in V}exp(u_w^Tv_c)} \\&=\frac{\partial}{\partial v_c}(logexp(u_o^Tv_c)-log\sum_{w\in V}exp(u_w^Tv_c)) \\&=\frac{\partial}{\partial v_c}(u_o^Tv_c-log\sum_{w\in V}exp(u_w^Tv_c))\\&=u_o-\frac{\sum_{w\in V}exp(u_w^Tv_c)u_w}{\sum_{w\in V}exp(u_w^Tv_c)} \end{aligned}$

偏导数可以移进求和中，对应上方公式的最后两行的推导 :
$\frac{\partial}{\partial x}\sum_iy_i=\sum_i\frac{\partial}{\partial x}y_i$

对上述结果重新排列如下 :

$\begin{aligned} u_o-\frac{\sum_{w\in V}exp(u_w^Tv_c)u_w}{\sum_{w\in V}exp(u_w^Tv_c)}&=u_o-\sum_{w\in V} \frac{exp(u_w^Tv_c)}{\sum_{w\in V}exp(u_w^Tv_c)}u_w\\&=u_o-\sum_{w\in V}P(w|c)u_w \end{aligned}$

第一项$u_0$是真正的上下文单词，第二项是预测的上下文单词。使用梯度下降法，模型的预测上下文将逐步接近真正的上下文。

对$u_0$进行偏微分计算(其中$u_o$是$u_w=o$的简写)，可知 :

$\frac{\partial}{\partial u_o}\sum_{w\in V}u_w^Tv_c=\frac{\partial}{\partial u_o}u_o^Tv_c=v_c$

$\begin{aligned} \frac{\partial}{\partial u_o}logP(o|c)&=\frac{\partial}{\partial u_o}log\frac{exp(u_o^Tv_c)}{\sum_{w\in V}exp(u_w^Tv_c)} \\&=\frac{\partial}{\partial u_o}(logexp(u_o^Tv_c)-log\sum_{w\in V}exp(u_w^Tv_c)) \\&=\frac{\partial}{\partial u_o}(u_o^Tv_c-log\sum_{w\in V}exp(u_w^Tv_c)) \\&=v_c-\frac{\sum_{w\in V}\frac{\partial}{\partial u_o}exp(u_w^Tv_c)}{\sum_{w\in V}exp(u_w^Tv_c)} \\&=v_c-\frac{exp(u_o^Tv_c)v_c}{\sum_{w\in V}exp(u_w^Tv_c)} \\&=v_c-\frac{exp(u_o^Tv_c)}{\sum_{w\in V}exp(u_w^Tv_c)}v_c \\&=v_c-P(o|c)v_c \\&=(1-P(o|c))v_c \end{aligned}$

从以上式子可看出，当$P(o|c) \rightarrow1$，即通过中心词$c$我们可以正确预测上下文词$o$，此时不需要调整$u_o$，反之，则要调整。

Notes 01 Introduction, SVD and Word2Vec

How to represent words?

Word Vectors

使用词向量编码单词，N维空间足够我们编码语言的所有语义，每一维度都会编码一些我们使用语言传递的信息。简单的one-hot向量无法给出单词间的相似性，我们需要将维度$|V|$减少至一个低纬度的子空间，来获得稠密的词向量，获得词之间的关系

SVD Based Methods

首先遍历一个很大的数据集和统计词的共现计数矩阵$X$，然后对矩阵$X$进行SVD分解得到$USV^T$。然后使用$U$的行来作为字典中所有词的词向量。
缺点 :

增加新的单词和语料库的大小会改变矩阵的维度
矩阵会非常的稀疏，因为很多词不会共现
矩阵维度会非常高
基于 SVD 的方法的计算复杂度很高
需要对$X$加入一些技巧处理来解决词频的极剧的不平衡
Iteration Based Methods - Word2vec
我们创建一个模型，该模型能够一次学习一个迭代，并最终对给定上下文的单词的概率进行编码，而不是像上面的方法存储一些大型数据集的全局信息。
我们设计一个模型，该模型的参数就是词向量。然后根据一个目标函数训练模型，在每次模型的迭代计算误差，并遵循一些更新规则，该规则具有惩罚造成错误的模型参数的作用，从而可以学习到词向量。这个方法可以追溯到1986年，我们称这个方法为“反向传播”，模型和任务越简单，训练它的速度就越快。基于迭代的方法一次捕获一个单词的共现情况，而不是像SVD方法那样直接捕获所有的共现计数。
已经很多人按照这个思路测试了不同的方法。[Collobert et al., 2011]设计的模型首先将每个单词转换为向量。对每个特定的任务（命名实体识别、词性标注等等），他们不仅训练模型的参数，同时也训练单词向量，计算出了非常好的词向量的同时取得了很好的性能。
Word2vec 是一个软件包实际上包含 :
两个算法 ：continuous bag-of-words（CBOW）和skip-gram。CBOW是根据中心词周围的上下文单词来预测该词的词向量。skip-gram则相反，是根据中心词预测周围上下文的词的概率分布。
两个训练方法 ：negative sampling和hierarchical softmax。Negative sampling通过抽取负样本来定义目标，hierarchical softmax通过使用一个有效的树结构来计算所有词的概率来定义目标。

该部分引出了Word2vec相关的知识点，基础知识通过刘建平博客学习过。